Пошук графа вширину!!!

Порядок виконання пошуку вширину

Поняття

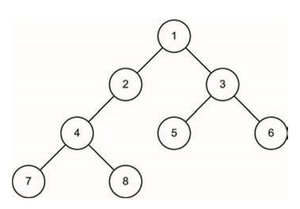
У пошуку вширину (Bread-first Search, BFS) ми розглядаємо граф з кореневого вузла в порядку збільшення відстані від кореня. Оскільки пошук по замовчанню є найближчим до кореня, BFS гарантовано знайде найкраще можливе рішення у незваженому графі, і тому він також є повним. Замість того, щоб копати глибоко в графі, прогресуючи далі і далі від кореня (як це відбувається з DFS), BFS перевіряє кожен вузол, найближчий до кореневого, перед тим, як спуститися на наступний рівень.

Впровадження BFS використовує чергу FIFO (first-in-first-out), відрізняється від реалізації стека (LIFO) для DFS. Оскільки нові вузли знаходяться під час пошуку, ці вузли перевіряються, якщо ж ціль не знайдено, нові вузли додаються до черги. Щоб продовжити пошук, найстаріший вузол видаляється (порядок FIFO). Використовуючи порядок FIFO для пошуку нового вузла, ми завжди перевіряємо найстаріші вузли першими, що призвело до «огляду вширину»

Недоліком BFS є те, що кожен вузол, в якому відбувається пошук, потрібно зберігати (складність простору - O (b^d)). Всю глибину дерева не треба оглядати, тому d в цьому контексті є глибиною рішення, а не максимальна глибина дерева. Складність часу також O (b^d). У практичних реалізаціях BFS та інших алгоритмів пошуку підтримується закритий список, який містить відвідані вузли на графі. Це дозволяє алгоритму ефективно оглядати граф без повторного відвідування вузлів. У реалізаціях, де граф має вагу, зберігання закритого списку неможливе.

Реалізація

#include <stdio.h> 
#include “graph.h” 
#include “queue.h” 
#define A 0
#define B 1 
#define C 2 
#define D 3 
#define E 4 
#define F 5 
#define G 6 
#define H 7 
int init_graph( graph_t *g_p ) 
{
  addEdge( g_p, A, B, 1 );
  addEdge( g_p, A, C, 1 );
  addEdge( g_p, B, D, 1 );
  addEdge( g_p, C, E, 1 );
  addEdge( g_p, C, F, 1 );
  addEdge( g_p, D, G, 1 );
  addEdge( g_p, D, H, 1 );
  return 0; 
}
void bfs( graph_t *g_p, int root, int goal ) 
{
  int node;
  int to;
  queue_t *q_p;
  q_p = createQueue( 10 );
  enQueue( q_p, root );
  while ( !isEmptyQueue(q_p) )
 {
    node = deQueue( q_p );
    printf(“%d\n”, node);
    if (node == goal) break;
    for (to = g_p->nodes-1 ; to > 0 ; to--) 
    {
      if (getEdge( g_p, node, to ) ) 
      {
        enQueue( q_p, to );
      }
    }
  }
  destroyQueue( q_p );
  return;
 } 
int main() 
{
  graph_t *g_p;
  g_p = createGraph( 8 );
  init_graph( g_p );
  bfs( g_p, 0, 7 );
  destroyGraph( g_p );
  return 0;
 }

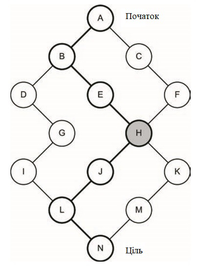
Двонаправлений пошук

Порядок виконання двонаправленого пошуку, що зустрівся на вузлі Н

Алгоритм двонаправленого пошуку є похідним від BFS, що оперує, виконуючи два пошуки вширину, один починаючи від кореневого вузла, а інший - від цільового вузла. Коли два пошукові запити зустрічаються посередині, шлях може бути відновлений від кореня до цілі. Зустріч пошуків визначається, коли знайдено спільний вузол. Це здійснюється шляхом збереження закритого списку відвіданих вузлів.

Двонаправлений пошук є цікавою ідеєю, але вимагає, щоб ми знали ціль, яку ми шукаємо на графі. Простота часу та простору для двонаправленого пошуку - це O (bd / 2), оскільки нам потрібно лише оглядати половину глибини дерева. Оскільки він базується на BFS, двонаправлений пошук є повним і оптимальним.

Допоміжний АРІ

Для демонстрації алгоритмів пошуку необхідний допоміжний АРІ, що включає перелічені функції:

/* Graph API */ 
graph_t *createGraph (int nodes ); 
void destroyGraph (graph_t *g_p ); 
void addEdge (graph_t *g_p, int from, int to, int value ); 
int getEdge (graph_t *g_p, int from, int to ); 
/* Stack API */ 
stack_t  *createStack (int depth ); 
void destroyStack (stack_t *s_p ); 
void pushStack (stack_t *s_p, int value ); 
int popStack (stack_t *s_p ); 
int isEmptyStack (stack_t *s_p ); 
/* Queue API */ 
queue_t  *createQueue (int depth ); 
void destroyQueue (queue_t *q_p ); 
void enQueue (queue_t *q_p, int value ); 
int deQueue (queue_t *q_p ); 
int isEmptyQueue (queue_t *q_p ); 
/* Priority Queue API */ 
pqueue_t *createPQueue (int depth );
void destroyPQueue (pqueue_t *q_p ); 
void enPQueue (pqueue_t *q_p, int value, int cost ); 
void dePQueue (pqueue_t *q_p, int *value, int *cost ); 
int isEmptyPQueue (pqueue_t *q_p ); 
int isFullPQueue (pqueue_t *q_p );

Виконав Романів Роман

Developed by Інститут Програмних Систем