Граф!!!

Поняття графа і властивості

Приклад неорієнтованого графа

Приклад орієнтованого графа

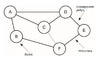
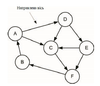
Граф - це скінченний набір вершин (або вузлів), які з'єднані зв'язками (або дугами). Цикл може існувати на графіку, де дуга (або зв'язок) може повернутись до вихідного вузла. Графи можуть бути неорієнтовані, де дуги не передбачають напрямку, або вони можуть бути направлені, де напрямок визначений дугою. Дуга також може мати вагу, що може бути пов'язана з шляхом. Кожен з цих графів також демонструє властивість підключення. Якщо кожен вузол підключений до кожного вузла дугою, граф повний.

Дерева і зв'язність

Зв'язним називають граф, в якому існує рівно один зв'язок між усіма можливими парами вузлів. Деревом називають такий зв'язний граф, в якому відсутні цикли

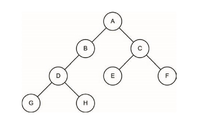
Репрезентація

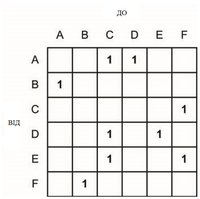
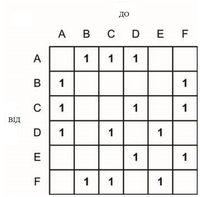
Одною з найпоширеніших форм представлення є матриця суміжності. Ця структура є просто матрицею N на N (де N - кількість вузлів у графі). Кожен елемент матриці визначає зв'язок (або суміжність) між відповідними вузлами (в залежності від стовпця і рядка). Нижче присутня матриця суміжності для раніше наведених прикладів графа (орієнтованого та неорієнтованого)

У простому випадку значення матриці просто визначають зв'язність вузлів у графі. У вагових графах, де дуги не всі рівні, значення в комірці може визначити вагу (вартість або відстань).

Списки суміжності також є популярною структурою, де кожен вузол містить список вузлів, з якими він з'єднується. Якщо граф розсіяний, така репрезентація може потребувати менше місця.

Виконав Романів Роман

Developed by Інститут Програмних Систем