Просторовий неінформований пошук!!!

Зміст
Пошук у фізичному просторі
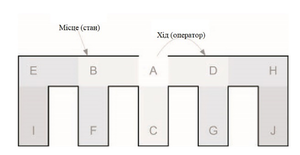
Розглянемо випадок пошуку у фізичному просторі. Наша початкова позиція ‘А’ з якої є три можливі шляхи, що ведуть до позицій ‘B’, ‘C’, або ‘D’. Місця, або ж стани, позначаються буквою. Біля кожного стану є можливість для рішення або дії. Дія (оператор) це просто крок від одного до іншого місця. Результатом в цій задачі є цільовий стан, або ж фізичне розташування, яке ми шукаємо.
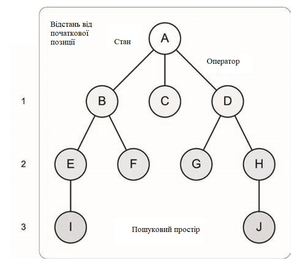
Цей пошуковий простір може бути зменшений до такого дерева. Пошуковий простір був звужений до необхідних місць на фізичній карті (карті станів) і переходів, які можливі між станами. Кожен вузол дерева є фізичним місцем, а зв’язки – переходами. Глибина дерева – це відстань від початкової позиції.
Пошук в просторі головоломки
Головоломка “Ханойська вежа” є цікавим прикладом для ілюстрування даного пошуку. Завданням цієї загадки є переміщення кількох дисків від одного кілка до іншого (по одному за раз), з рядом обмежень, які необхідно виконати. Кожен диск має унікальний розмір, і більшому диска не дозволено перебувати над меншим. Початковий стан головоломки такий, коли всі диски перебувають на одному кілку у зростаючому порядку. Нашою метою (рішенням) є переміщення всіх дисків до останнього кілка.
Як і в багатьох станах простору, існують потенційні переходи, які не є можливими. Наприклад, ми можемо лише перемістити кілок, який не має іншого над собою. Крім того, ми не можемо перемістити великий диск на менший диск (хоча ми можемо перемістити будь-який диск до порожнього кілка) Таким чином, простір можливих операторів обмежується лише дозволеними рухами. Стан простору також може бути обмежений рухами, які ще не виконані для певного піддерева.
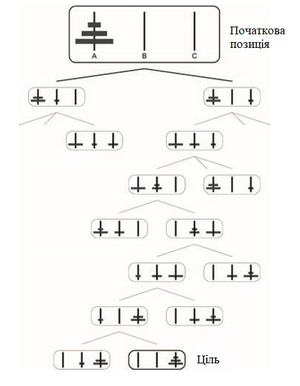
Розглянемо наше початкове положення з рисунка. Єдиний диск, який може рухатися, - це малий диск у верхній частині кілка A. Для цього диска можливі лише два дозволених ходи: з кілка A до кілка B, або до кілка C. В свою чергу, з цього стану існує три потенційних ходи:
- Перемістити малий диск з кілка С до кілка В
- Перемістити малий диск з кілка С до кілка А
- Перемістити середній диск з кілька А до кілка В
Перший хід (малий диск з кілка C до кілка B) не є потенційним кроком, оскільки ми щойно перенесли цей диск до кілка C (порожній кілок). Переміщення вдруге не має сенсу, оскільки цей крок міг бути зроблений під час попереднього переходу.
Другий крок також не є корисним, тому що є оберненим попереднім ходом. Це залишає один дійсний крок, середній диск з кілка A до кілка B. Переходи від цього стану стають складнішими, оскільки можливі рухи, що віддалятимуть нас від розв’язку.
Коли наша послідовність рухів веде з вихідної позиції до мети, це розв’язок. Цільовий стан сам по собі не цікавий, але, що цікаво, так це послідовність дій, що привела нас до цільового стану. Конфігурація цієї головоломки може бути задана від цільової позиції, з поверненням назад до початкової позиції.
Пошук в просторі змагальних ігор
Досить цікавим є використання пошукового простору в іграх. Також відомі як ігрові дерева, структури перелічують можливі кроки кожного гравця, що дозволяє алгоритму пошуку знайти ефективну стратегію виграшу.
Гра "Нім"
Нім - це стратегічна гра для двох гравців. Гра побудована на переміщенні певної множини об'єктів між кількома купками. Переможцем стає гравець, що забрав останній об'єкт.
Гравця, який виграє, можна передбачити, опираючись на кількість об’єктів, їх куп, та інформацію, хто ходить першим.
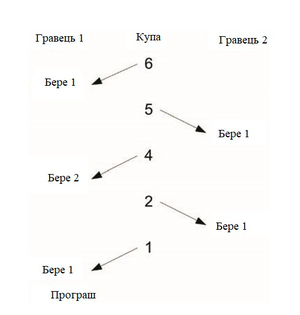
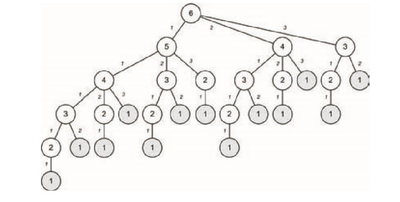
Давайте розглянемо приклад, щоб зрозуміти, як грати в Нім. Почнемо з однієї маленької купи, щоб обмежити кількість необхідних рухів. На рисунку ілюструється коротка гра з купою з шести об'єктів. Кожен гравець може взяти один, два, або три об'єкти з купи. У цьому прикладі гравець 1 починає гру, але закінчує гру з втратою. Якщо б гравець 1 взяв три об’єкти у своєму другому кроці, гравець 2 залишився б з одним, що б призвело до перемоги для гравця 1.
Ігрове дерево робить цю інформацію видимою, як це показано на рисунку. Примітка у дереві, що гравець 1 повинен прибрати один об’єкт з купи для продовження гри. Якщо гравець 1 видаляє об’єкт два або три з купи, гравець 2 може виграти, якщо гратиме оптимально. Затінені вузли в дереві ілюструють втрату позицій для гравця, який повинен обирати наступним (і в усіх випадках єдиним вибором залишалося взяти останній об'єкт).
Зауважте, що глибина дерева визначає тривалість гри (кількість ходів). В дереві мається на увазі, що затемнений вузол - це останній крок, і гравець, який робить цей рух, програє гру. На щастя, дерево можна оптимізувати, видаливши дублікати піддерев, що приведе до набагато меншого дерева.
Виконав Романів Роман
Developed by Інститут Програмних Систем