Відмінності між версіями «Пошук графа вширину»!!!

111 (обговорення • внесок) (→Двонаправлений пошук) |
111 (обговорення • внесок) (→Пошук вширину з критерієм ваги) |
||
| Рядок 80: | Рядок 80: | ||
Пошук з критерієм ваги (вартості) (UCS) можна застосувати, щоб знайти найнижчу вартість через [[Граф|граф]], зберігаючи упорядкований список вузлів у порядку зниження ваги. Це дозволяє нам оцінити найменший рівень витрат з самого початку. | Пошук з критерієм ваги (вартості) (UCS) можна застосувати, щоб знайти найнижчу вартість через [[Граф|граф]], зберігаючи упорядкований список вузлів у порядку зниження ваги. Це дозволяє нам оцінити найменший рівень витрат з самого початку. | ||
| − | Алгоритм UCS використовує накопичену вартість шляху для визначення шляху для оцінки. Черга пріоритетів (відсортована від найменшої вартості до найбільшої) містить вузли для оцінювання. Оскільки діти вузлів оцінюються, ми додаємо їхню вартість до вузла з сукупною сумою поточного шляху. Цей вузол потім додається до черги, а коли всі діти оцінюються, то черга сортується в порядку зростання вартості. Коли першим елементом у черзі на пріоритет є цільовий вузол, то знайдено найкраще рішення. | + | [[Алгоритм|Алгоритм]] UCS використовує накопичену вартість шляху для визначення шляху для оцінки. Черга пріоритетів (відсортована від найменшої вартості до найбільшої) містить вузли для оцінювання. Оскільки діти вузлів оцінюються, ми додаємо їхню вартість до вузла з сукупною сумою поточного шляху. Цей вузол потім додається до черги, а коли всі діти оцінюються, то черга сортується в порядку зростання вартості. Коли першим елементом у черзі на пріоритет є цільовий вузол, то знайдено найкраще рішення. |
UCS є оптимальним і може бути повним, але тільки в тому випадку, якщо вартість дуг невід'ємна (сумарна вартість маршруту завжди зростає). Складність часу та простору є такою ж, як BFS, O (b^d) для кожного. | UCS є оптимальним і може бути повним, але тільки в тому випадку, якщо вартість дуг невід'ємна (сумарна вартість маршруту завжди зростає). Складність часу та простору є такою ж, як BFS, O (b^d) для кожного. | ||
| Рядок 89: | Рядок 89: | ||
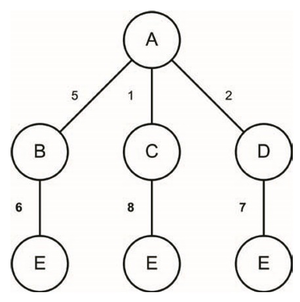
На першому кроці початковий вузол був доданий до черги для пріоритетів, з вартістю нуль. На другому кроці кожний із трьох пов'язаних вузлів оцінюється та додається в чергу пріоритету. Коли жоден дочірній вузол не доступний для оцінки, черга пріоритетів сортується, щоб розмістити їх у порядку зростання вартості. | На першому кроці початковий вузол був доданий до черги для пріоритетів, з вартістю нуль. На другому кроці кожний із трьох пов'язаних вузлів оцінюється та додається в чергу пріоритету. Коли жоден дочірній вузол не доступний для оцінки, черга пріоритетів сортується, щоб розмістити їх у порядку зростання вартості. | ||
| − | На третьому етапі оцінюються дочірні вузли С. У цьому випадку ми знаходимо бажану ціль (E), але оскільки накопичена ціна шляху становить вісім, вона закінчується в кінці черги. Для четвертого етапу ми оцінюємо вузол D та знову шукаємо цільовий вузол. Ціна шляху дорівнює семи, що все ще перевершує наш вузол B у черзі. Нарешті, на п’ятому етапі, оцінюється вузол В. Цільовий вузол знайдено знову, при цьому вартість маршруту становить шість. Черга пріоритету тепер містить цільовий вузол у верхній частині, що означає, що на наступній ітерації циклу алгоритм вийде з шляху A-> B-> E (працює назад від цільового вузла до початкового вузла). | + | На третьому етапі оцінюються дочірні вузли С. У цьому випадку ми знаходимо бажану ціль (E), але оскільки накопичена ціна шляху становить вісім, вона закінчується в кінці черги. Для четвертого етапу ми оцінюємо вузол D та знову шукаємо цільовий вузол. Ціна шляху дорівнює семи, що все ще перевершує наш вузол B у черзі. Нарешті, на п’ятому етапі, оцінюється вузол В. Цільовий вузол знайдено знову, при цьому вартість маршруту становить шість. Черга пріоритету тепер містить цільовий вузол у верхній частині, що означає, що на наступній ітерації циклу [[Алгоритм|алгоритм]] вийде з шляху A-> B-> E (працює назад від цільового вузла до початкового вузла). |
Щоб обмежити розмір черги для пріоритетів, можна стерти записи, які є надлишковими. Наприклад, на кроці 4, запис про E (8) можна було б безпечно видалити, оскільки існує інший шлях, який має нижчу вартість (E (7)). | Щоб обмежити розмір черги для пріоритетів, можна стерти записи, які є надлишковими. Наприклад, на кроці 4, запис про E (8) можна було б безпечно видалити, оскільки існує інший шлях, який має нижчу вартість (E (7)). | ||
Версія за 23:51, 16 лютого 2018
Зміст
Пошук вширину
Поняття
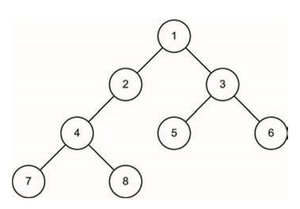
У пошуку вширину (Bread-first Search, BFS) ми розглядаємо граф з кореневого вузла в порядку збільшення відстані від кореня. Оскільки пошук по замовчанню є найближчим до кореня, BFS гарантовано знайде найкраще можливе рішення у незваженому графі, і тому він також є повним. Замість того, щоб копати глибоко в графі, прогресуючи далі і далі від кореня (як це відбувається з DFS), BFS перевіряє кожен вузол, найближчий до кореневого, перед тим, як спуститися на наступний рівень.
Впровадження BFS використовує чергу FIFO (first-in-first-out), відрізняється від реалізації стека (LIFO) для DFS. Оскільки нові вузли знаходяться під час пошуку, ці вузли перевіряються, якщо ж ціль не знайдено, нові вузли додаються до черги. Щоб продовжити пошук, найстаріший вузол видаляється (порядок FIFO). Використовуючи порядок FIFO для пошуку нового вузла, ми завжди перевіряємо найстаріші вузли першими, що призвело до «огляду вширину»
Недоліком BFS є те, що кожен вузол, в якому відбувається пошук, потрібно зберігати (складність простору - O (b^d)). Всю глибину дерева не треба оглядати, тому d в цьому контексті є глибиною рішення, а не максимальна глибина дерева. Складність часу також O (b^d). У практичних реалізаціях BFS та інших алгоритмів пошуку підтримується закритий список, який містить відвідані вузли на графі. Це дозволяє алгоритму ефективно оглядати граф без повторного відвідування вузлів. У реалізаціях, де граф має вагу, зберігання закритого списку неможливе.
Реалізація
#include <stdio.h>
#include “graph.h”
#include “queue.h”
#define A 0
#define B 1
#define C 2
#define D 3
#define E 4
#define F 5
#define G 6
#define H 7
int init_graph( graph_t *g_p )
{
addEdge( g_p, A, B, 1 );
addEdge( g_p, A, C, 1 );
addEdge( g_p, B, D, 1 );
addEdge( g_p, C, E, 1 );
addEdge( g_p, C, F, 1 );
addEdge( g_p, D, G, 1 );
addEdge( g_p, D, H, 1 );
return 0;
}
void bfs( graph_t *g_p, int root, int goal )
{
int node;
int to;
queue_t *q_p;
q_p = createQueue( 10 );
enQueue( q_p, root );
while ( !isEmptyQueue(q_p) )
{
node = deQueue( q_p );
printf(“%d\n”, node);
if (node == goal) break;
for (to = g_p->nodes-1 ; to > 0 ; to--)
{
if (getEdge( g_p, node, to ) )
{
enQueue( q_p, to );
}
}
}
destroyQueue( q_p );
return;
}
int main()
{
graph_t *g_p;
g_p = createGraph( 8 );
init_graph( g_p );
bfs( g_p, 0, 7 );
destroyGraph( g_p );
return 0;
}
Двонаправлений пошук
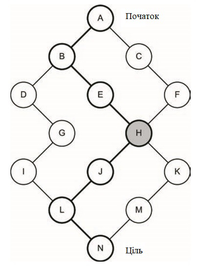
Алгоритм двонаправленого пошуку є похідним від BFS, що оперує, виконуючи два пошуки вширину, один починаючи від кореневого вузла, а інший - від цільового вузла. Коли два пошукові запити зустрічаються посередині, шлях може бути відновлений від кореня до цілі. Зустріч пошуків визначається, коли знайдено спільний вузол. Це здійснюється шляхом збереження закритого списку відвіданих вузлів.
Двонаправлений пошук є цікавою ідеєю, але вимагає, щоб ми знали ціль, яку ми шукаємо на графі. Простота часу та простору для двонаправленого пошуку - це O (bd / 2), оскільки нам потрібно лише оглядати половину глибини дерева. Оскільки він базується на BFS, двонаправлений пошук є повним і оптимальним.
Пошук вширину з критерієм ваги
Поняття
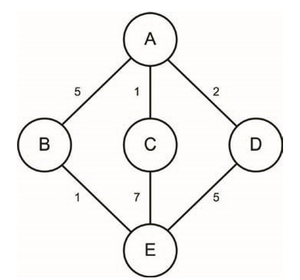
Пошук з критерієм ваги (вартості) (UCS) можна застосувати, щоб знайти найнижчу вартість через граф, зберігаючи упорядкований список вузлів у порядку зниження ваги. Це дозволяє нам оцінити найменший рівень витрат з самого початку.
Алгоритм UCS використовує накопичену вартість шляху для визначення шляху для оцінки. Черга пріоритетів (відсортована від найменшої вартості до найбільшої) містить вузли для оцінювання. Оскільки діти вузлів оцінюються, ми додаємо їхню вартість до вузла з сукупною сумою поточного шляху. Цей вузол потім додається до черги, а коли всі діти оцінюються, то черга сортується в порядку зростання вартості. Коли першим елементом у черзі на пріоритет є цільовий вузол, то знайдено найкраще рішення.
UCS є оптимальним і може бути повним, але тільки в тому випадку, якщо вартість дуг невід'ємна (сумарна вартість маршруту завжди зростає). Складність часу та простору є такою ж, як BFS, O (b^d) для кожного.
Перебіг пошуку
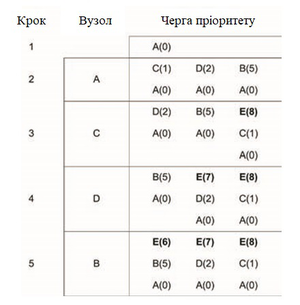
На першому кроці початковий вузол був доданий до черги для пріоритетів, з вартістю нуль. На другому кроці кожний із трьох пов'язаних вузлів оцінюється та додається в чергу пріоритету. Коли жоден дочірній вузол не доступний для оцінки, черга пріоритетів сортується, щоб розмістити їх у порядку зростання вартості.
На третьому етапі оцінюються дочірні вузли С. У цьому випадку ми знаходимо бажану ціль (E), але оскільки накопичена ціна шляху становить вісім, вона закінчується в кінці черги. Для четвертого етапу ми оцінюємо вузол D та знову шукаємо цільовий вузол. Ціна шляху дорівнює семи, що все ще перевершує наш вузол B у черзі. Нарешті, на п’ятому етапі, оцінюється вузол В. Цільовий вузол знайдено знову, при цьому вартість маршруту становить шість. Черга пріоритету тепер містить цільовий вузол у верхній частині, що означає, що на наступній ітерації циклу алгоритм вийде з шляху A-> B-> E (працює назад від цільового вузла до початкового вузла).
Щоб обмежити розмір черги для пріоритетів, можна стерти записи, які є надлишковими. Наприклад, на кроці 4, запис про E (8) можна було б безпечно видалити, оскільки існує інший шлях, який має нижчу вартість (E (7)).
Реалізація
#include <stdio.h>
#include “graph.h”
#include “pqueue.h”
#define A 0
#define B 1
#define C 2
#define D 3
#define E 4
int init_graph( graph_t *g_p )
{
addEdge( g_p, A, B, 5 );
addEdge( g_p, A, C, 1 );
addEdge( g_p, A, D, 2 );
addEdge( g_p, B, E, 1 );
addEdge( g_p, C, E, 7 );
addEdge( g_p, D, E, 5 );
return 0;
}
void ucs( graph_t *g_p, int root, int goal )
{
int node, cost, child_cost;
int to; pqueue_t *q_p;
q_p = createPQueue( 7 );
enPQueue( q_p, root, 0 );
while ( !isEmptyPQueue(q_p) )
{
dePQueue( q_p, &node, &cost );
if (node == goal)
{
printf(“cost %d\n”, cost);
return;
}
for (to = g_p->nodes-1 ; to > 0 ; to--)
{
child_cost = getEdge( g_p, node, to );
if (child_cost)
{
enPQueue( q_p, to, (child_cost+cost) );
}
}
}
destroyPQueue( q_p );
return;
}
int main()
{
graph_t *g_p;
g_p = createGraph( 6 );
init_graph( g_p );
ucs( g_p, A, E );
destroyGraph( g_p );
return 0;
}
Допоміжний АРІ
Для демонстрації алгоритмів пошуку необхідний допоміжний АРІ, що включає перелічені функції:
/* Graph API */ graph_t *createGraph (int nodes ); void destroyGraph (graph_t *g_p ); void addEdge (graph_t *g_p, int from, int to, int value ); int getEdge (graph_t *g_p, int from, int to ); /* Stack API */ stack_t *createStack (int depth ); void destroyStack (stack_t *s_p ); void pushStack (stack_t *s_p, int value ); int popStack (stack_t *s_p ); int isEmptyStack (stack_t *s_p ); /* Queue API */ queue_t *createQueue (int depth ); void destroyQueue (queue_t *q_p ); void enQueue (queue_t *q_p, int value ); int deQueue (queue_t *q_p ); int isEmptyQueue (queue_t *q_p ); /* Priority Queue API */ pqueue_t *createPQueue (int depth ); void destroyPQueue (pqueue_t *q_p ); void enPQueue (pqueue_t *q_p, int value, int cost ); void dePQueue (pqueue_t *q_p, int *value, int *cost ); int isEmptyPQueue (pqueue_t *q_p ); int isFullPQueue (pqueue_t *q_p );Developed by Інститут Програмних Систем