Відмінності між версіями «Пошук графа вглибину»!!!

Матеріал з wiki
Перейти до: навігація, пошук
Onpage keywords chain search with * wildcard. Example: sear* my nam* will find Searh my names and search my Name

(Створена сторінка: == Пошук вглибину == Файл:Graph_depth_first_search_flow.png|300px|thumb|right|Порядок виконання пошуку вглибину...)
 
(→‎Допоміжний АРІ)
 
(не показано 14 проміжних версій цього учасника)
Рядок 2: Рядок 2:
 
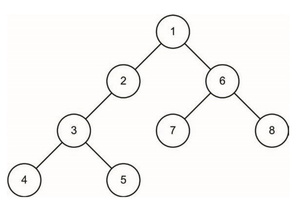
[[Файл:Graph_depth_first_search_flow.png|300px|thumb|right|Порядок виконання пошуку вглибину в малому дереві]]
 
[[Файл:Graph_depth_first_search_flow.png|300px|thumb|right|Порядок виконання пошуку вглибину в малому дереві]]
 
=== Поняття ===
 
=== Поняття ===
−
Алгоритм пошуку вглибину (Depth-First Search, DFS) - це метод пошуку графа, який починається з кореневого вузла, і оглядає кожну гілку на найглибшому рівні, перш ніж відслідковувати попередньо нерозвідані гілки. Знайдені, але ще не перевірені вузли зберігаються в черзі LIFO (стек).
+
[[Алгоритм|Алгоритм]] пошуку вглибину (Depth-First Search, DFS) - це метод пошуку [[Граф|графа]], який починається з кореневого вузла, і оглядає кожну гілку на найглибшому рівні, перш ніж відслідковувати попередньо нерозвідані гілки. Знайдені, але ще не перевірені вузли зберігаються в черзі LIFO (стек).
  
−
Складність простору для DFS - це O (bd), де складність часу геометрична (O (b^d)). Це може бути великою проблемою для глибоких розгалужених графіків, оскільки алгоритм буде продовжувати до максимальної глибини графа. Якщо в графі присутні цикли, DFS буде слідувати цим циклам безкінечно. З цієї причини алгоритм DFS не є повним, оскільки цикли можуть не дати алгоритму виявити ціль. Якщо на графі немає циклів, то алгоритм повний (завжди знайде цільовий вузол). Алгоритм DFS не є оптимальним, але може ним стати, за допомогою перевірки шляху (щоб забезпечити найкоротший шлях до мети).
+
Складність простору для DFS - це O (bd), де складність часу геометрична (O (b^d)). Це може бути великою проблемою для глибоких розгалужених [[Граф|графів]], оскільки [[Алгоритм|алгоритм]] буде продовжувати до максимальної глибини [[Граф|графа]]. Якщо в [[Граф|графі]] присутні цикли, DFS буде слідувати цим циклам безкінечно. З цієї причини алгоритм DFS не є повним, оскільки цикли можуть не дати алгоритму виявити ціль. Якщо на [[Граф|графі]] немає циклів, то алгоритм повний (завжди знайде цільовий вузол). Алгоритм DFS не є оптимальним, але може ним стати, за допомогою перевірки шляху (щоб забезпечити найкоротший шлях до мети).
  
 
=== Реалізація ===
 
=== Реалізація ===
−
Алгоритми графів можуть бути реалізовані як рекурсивно, так і за допомогою стеків для підтримки списку вузлів, які необхідно перерахувати. У нижче наведеному прикладі алгоритм DFS реалізується за допомогою стека LIFO. Також наведено необхідний допоміжний АРІ.
+
Алгоритми [[Граф|графів]] можуть бути реалізовані як рекурсивно, так і за допомогою стеків для підтримки списку вузлів, які необхідно перерахувати. У нижче наведеному прикладі алгоритм DFS реалізується за допомогою стека LIFO. Також наведено необхідний допоміжний АРІ.
  
 
  <nowiki>
 
  <nowiki>
Рядок 66: Рядок 66:
 
</nowiki>
 
</nowiki>
  
−
== Пошук з обмеженням глибини ==
+
== Допоміжний АРІ ==
−
[[Файл:Depth_limited_search_flow.png|300px|thumb|right|Порядок виконання пошуку з обмеженням глибини 2]]
+
−
=== Поняття ===
+
−
Пошук з обмеженням глибини (Depth-Limited Search, DLS) – це модифікація пошуку вглибину, яка мінімізує глибину, на яку може йти алгоритм пошуку. Крім того, що починається з кореневого та цільового вузлів, передбачається, що алгоритм не спускається нижче певного рівня.
+
−
Ця модифікація зберігає алгоритм від безкінечних циклів, зупиняючи пошук після попередньо встановленої глибини.
+
−
 
+
−
Хоча алгоритм усуває можливість нескінченного циклу у графі, він також зменшує область пошуку. Якщо цільовий вузол був одним з вузлів із позначкою "X", його не було б знайдено, зробивши алгоритм пошуку неповним. Алгоритм може бути повним, якщо глибина пошуку залежить від самого дерева (у цьому випадку d дорівнює трьом). Техніка також не є оптимальною, оскільки може бути знайдений перший шлях замість найкоротшого.
+
−
 
+
−
Час і простір обмеженого по глибині пошуку аналогічні DFS, з якого виводиться цей алгоритм. Складність простору - це O (bd), а складність часу - O (b^d), але в цьому випадку d є глибиною пошуку, а не графа.
+
−
 
+
−
=== Реалізація ===
+
−
<nowiki>
+
−
#include <stdio.h>
+
−
#include “graph.h”
+
−
#include “stack.h”
+
−
#define A 0
+
−
#define B 1
+
−
#define C 2
+
−
#define D 3
+
−
#define E 4
+
−
#define F 5
+
−
#define G 6
+
−
#define H 7
+
−
int init_graph( graph_t *g_p )
+
−
{
+
−
  addEdge( g_p, A, B, 1 );
+
−
  addEdge( g_p, A, C, 1 );
+
−
  addEdge( g_p, B, D, 1 );
+
−
  addEdge( g_p, C, E, 1 );
+
−
  addEdge( g_p, C, F, 1 );
+
−
  addEdge( g_p, D, G, 1 );
+
−
  addEdge( g_p, D, H, 1 );
+
−
  return 0;
+
−
}
+
−
void dls( graph_t *g_p, int root, int goal, int limit )
+
−
{
+
−
  int node, depth, to;
+
−
  stack_t *s_p, *sd_p;
+
−
  s_p = createStack( 10 );
+
−
  sd_p = createStack( 10 );
+
−
  pushStack( s_p, root );
+
−
  pushStack( sd_p, 0 );
+
−
  while ( !isEmptyStack(s_p) )
+
−
  {
+
−
    node = popStack( s_p );
+
−
    depth = popStack( sd_p );
+
−
    printf(“%d (depth %d)\n”, node, depth);
+
−
    if (node == goal) break;
+
−
    if (depth < limit)
+
−
    {
+
−
      for (to = g_p->nodes-1 ; to > 0 ; to--)
+
−
      {
+
−
        if (getEdge( g_p, node, to ) )
+
−
        {
+
−
          pushStack( s_p, to );
+
−
          pushStack( sd_p, depth+1 );
+
−
        }
+
−
      }
+
−
    }
+
−
  }
+
−
  destroyStack( s_p );
+
−
  destroyStack( sd_p );
+
−
  return;
+
−
}
+
−
int main()
+
−
{
+
−
  graph_t *g_p;  g_p = createGraph( 8 );
+
−
  init_graph( g_p );
+
−
  dls( g_p, 0, 5, 2 );
+
−
  destroyGraph( g_p );
+
−
  return 0;
+
−
}
+
−
 
+
−
</nowiki>
+
−
 
+
−
== Пошук з ітеративним заглибленням ==
+
−
[[Файл:Iterative_deepening_search_flow.png|300px|thumb|right|Порядок виконання пошуку з обмеженням глибини 2]]
+
−
=== Поняття ===
+
−
Пошук з ітеративним заглибленням (Iterative Deepening Search, IDS) – це похідний від DLS алгоритм, що поєднує в собі особливості пошуку вглибину з та пошуку вширину. IDS працює, виконуючи пошуки DLS із збільшеною глибиною, доки не буде знайдено ціль.
+
−
Мінімізуючи глибину пошуку, ми змушуємо алгоритм шукати вширину графа. Якщо ціль не знайдено, збільшується глибина, яку алгоритму дозволено шукати, і він запускається знову.
+
−
 
+
−
IDS є зручним, тому що він не схильний до зациклення (характеристика DLS, на якій вона заснована). Він також знаходить ціль, найближчу до кореневого вузла, як і алгоритм BFS (який буде детально описано далі). З цієї причини це найкращий алгоритм, коли глибина рішення невідома.
+
−
 
+
−
Складність часу для IDS ідентична DFS і DLS, O (b^d). Простір складності IDS - O (bd). Навідмінно від DFS та DLS, IDS завжди знайде найкраще рішення, тому він є повним і оптимальним.
+
−
 
+
−
=== Реалізація ===
+
−
<nowiki>
+
−
#include <stdio.h>
+
−
#include “graph.h”
+
−
#include “stack.h”
+
−
#define A 0
+
−
#define B 1
+
−
#define C 2
+
−
#define D 3
+
−
#define E 4
+
−
#define F 5
+
−
#define G 6
+
−
#define H 7
+
−
int init_graph( graph_t *g_p )
+
−
{
+
−
  addEdge( g_p, A, B, 1 );
+
−
  addEdge( g_p, A, C, 1 );
+
−
  addEdge( g_p, B, D, 1 );
+
−
  addEdge( g_p, C, E, 1 );
+
−
  addEdge( g_p, C, F, 1 );
+
−
  addEdge( g_p, D, G, 1 );
+
−
  addEdge( g_p, D, H, 1 );
+
−
  return 0;
+
−
}
+
−
int dls( graph_t *g_p, int root, int goal, int limit )
+
−
{
+
−
  int node, depth;
+
−
  int to;
+
−
  stack_t *s_p, *sd_p;
+
−
  s_p = createStack( 10 );
+
−
  sd_p = createStack( 10 );
+
−
  pushStack( s_p, root );
+
−
  pushStack( sd_p, 0 );
+
−
  while ( !isEmptyStack(s_p) )
+
−
  {
+
−
    node = popStack( s_p );
+
−
    depth = popStack( sd_p );
+
−
    printf(“%d (depth %d)\n”, node, depth);
+
−
    if (node == goal) return 1;
+
−
    if (depth < limit)
+
−
    {
+
−
      for (to = g_p->nodes-1 ; to > 0 ; to--)
+
−
      {
+
−
        if (getEdge( g_p, node, to ) )
+
−
        {
+
−
          pushStack( s_p, to );
+
−
          pushStack( sd_p, depth+1 );
+
−
        }
+
−
      }
+
−
    }
+
−
  }
+
−
  destroyStack( s_p );
+
−
  destroyStack( sd_p );
+
−
  return 0;
+
−
}
+
−
int main()
+
−
{
+
−
  graph_t *g_p;
+
−
  int    status, depth;
+
−
  g_p = createGraph( 8 );
+
−
  init_graph( g_p );
+
−
  depth = 1;
+
−
  while (1)
+
−
  {
+
−
    status = dls( g_p, 0, 5, depth );
+
−
    if (status == 1) break;
+
−
    else depth++;
+
−
  }
+
−
  destroyGraph( g_p );
+
−
  return 0;
+
−
}
+
−
</nowiki>
+
−
 
+
−
 
+
−
=== Допоміжний АРІ ===
+
 
Для демонстрації алгоритмів пошуку необхідний допоміжний АРІ, що включає перелічені функції:
 
Для демонстрації алгоритмів пошуку необхідний допоміжний АРІ, що включає перелічені функції:
 
  <nowiki>
 
  <nowiki>
Рядок 252: Рядок 93:
 
int isEmptyPQueue (pqueue_t *q_p );  
 
int isEmptyPQueue (pqueue_t *q_p );  
 
int isFullPQueue (pqueue_t *q_p );</nowiki>
 
int isFullPQueue (pqueue_t *q_p );</nowiki>
 +
 +
'''Виконав [[Романів Роман]]'''

Поточна версія на 01:04, 19 лютого 2018

Пошук вглибину

Порядок виконання пошуку вглибину в малому дереві

Поняття

Алгоритм пошуку вглибину (Depth-First Search, DFS) - це метод пошуку графа, який починається з кореневого вузла, і оглядає кожну гілку на найглибшому рівні, перш ніж відслідковувати попередньо нерозвідані гілки. Знайдені, але ще не перевірені вузли зберігаються в черзі LIFO (стек).

Складність простору для DFS - це O (bd), де складність часу геометрична (O (b^d)). Це може бути великою проблемою для глибоких розгалужених графів, оскільки алгоритм буде продовжувати до максимальної глибини графа. Якщо в графі присутні цикли, DFS буде слідувати цим циклам безкінечно. З цієї причини алгоритм DFS не є повним, оскільки цикли можуть не дати алгоритму виявити ціль. Якщо на графі немає циклів, то алгоритм повний (завжди знайде цільовий вузол). Алгоритм DFS не є оптимальним, але може ним стати, за допомогою перевірки шляху (щоб забезпечити найкоротший шлях до мети).

Реалізація

Алгоритми графів можуть бути реалізовані як рекурсивно, так і за допомогою стеків для підтримки списку вузлів, які необхідно перерахувати. У нижче наведеному прикладі алгоритм DFS реалізується за допомогою стека LIFO. Також наведено необхідний допоміжний АРІ. 

#include <stdio.h> 
#include “graph.h” 
#include “stack.h” 
#define A 0 
#define B 1
#define C 2 
#define D 3 
#define E 4 
#define F 5 
#define G 6 
#define H 7 
int init_graph( graph_t *g_p ) 
{
  addEdge( g_p, A, B, 1 );
  addEdge( g_p, A, C, 1 );
  addEdge( g_p, B, D, 1 );
  addEdge( g_p, C, E, 1 );
  addEdge( g_p, C, F, 1 );
  addEdge( g_p, D, G, 1 );
  addEdge( g_p, D, H, 1 );
  return 0; 
} 
void dfs( graph_t *g_p, int root, int goal ) 
{
  int node;
  int to;
  stack_t *s_p;
  s_p = createStack( 10 );
  pushStack( s_p, root );
  while ( !isEmptyStack(s_p) )
  {
    node = popStack( s_p );
    printf(“%d\n”, node);
    if (node == goal) break;
    for (to = g_p->nodes-1 ; to > 0 ; to--)
    {
      if (getEdge( g_p, node, to ) ) 
      {
        pushStack( s_p, to );
      }
    }
  }
  destroyStack( s_p );
  return;
 } 
int main() 
{
  graph_t *g_p;
  g_p = createGraph( 8 );
  init_graph( g_p );
  dfs( g_p, 0, 5 );
  destroyGraph( g_p );
  return 0;
}

Допоміжний АРІ

Для демонстрації алгоритмів пошуку необхідний допоміжний АРІ, що включає перелічені функції: 

/* Graph API */ 
graph_t *createGraph (int nodes ); 
void destroyGraph (graph_t *g_p ); 
void addEdge (graph_t *g_p, int from, int to, int value ); 
int getEdge (graph_t *g_p, int from, int to ); 
/* Stack API */ 
stack_t  *createStack (int depth ); 
void destroyStack (stack_t *s_p ); 
void pushStack (stack_t *s_p, int value ); 
int popStack (stack_t *s_p ); 
int isEmptyStack (stack_t *s_p ); 
/* Queue API */ 
queue_t  *createQueue (int depth ); 
void destroyQueue (queue_t *q_p ); 
void enQueue (queue_t *q_p, int value ); 
int deQueue (queue_t *q_p ); 
int isEmptyQueue (queue_t *q_p ); 
/* Priority Queue API */ 
pqueue_t *createPQueue (int depth );
void destroyPQueue (pqueue_t *q_p ); 
void enPQueue (pqueue_t *q_p, int value, int cost ); 
void dePQueue (pqueue_t *q_p, int *value, int *cost ); 
int isEmptyPQueue (pqueue_t *q_p ); 
int isFullPQueue (pqueue_t *q_p );

Виконав Романів Роман

Developed by Інститут Програмних Систем
Отримано з http://wiki.isofts.kiev.ua/index.php?title=Пошук_графа_вглибину&oldid=2342