Загадка Восьми!!!

Загадка Восьми
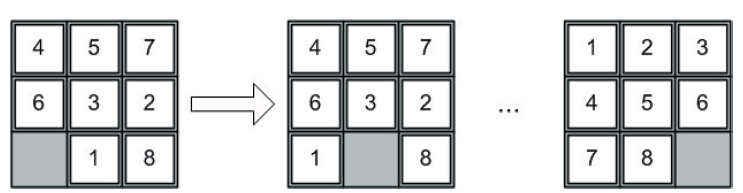
Малюнок 3.4: Задача Восьми та демонстрація переходу з вхідної конфігурації до кінцевої (не включає кожен єтап).
Хоча A * успішно застосовується до проблемних доменів, таких як конфігурація, ми застосуємо його тут, що називається "Загадка восьми" (також відомий як N від M, або n^2-1 загадка черпиць). Ця особлива варіація головоломки складається з восьми черепиць в сітці 3х3. В одному місці немає плитки, що можна використовувати для переміщення інших плиток для переходу від однієї конфігурації до іншої (див. Малюнок 3.4).
Зверніть увагу на малюнку 3.4, що є можливі дві дії. Плитка '1' може рухатися вліво, а плитка '6' може рухатися вниз. Остаточна мета конфігурації показана справа. Зауважте, що це один варіант мети, і той, який ми будемо використовувати тут.
Загадка Восьми- це цікаво, тому що важко вирішити проблему, але та, що вивчається довго, і тому дуже добре зрозуміла. [Archer 1999] Наприклад, кількість можливих конфігурацій сітки Загадки Восьми (n * n)!, але лише половина з них є легальними конфігураціями.
Підказка У 1870-х роках Загадка П'ятнадцяти (4 на 4 варіанти головоломки N по M) перетворилися на загальне захоплення так само, як кубик Рубіка 1970-х та 80-х років.
У середньому 22 кроки потрібні для вирішення 3-х варіантів головоломки. Але, розглядаючи 22 як середню глибину дерева, із середнім коефіцієнтом розгалуження 2,67, може бути оцінено 2,4 трильйони не унікальних плиток.
Уявлення Загадки Восьми
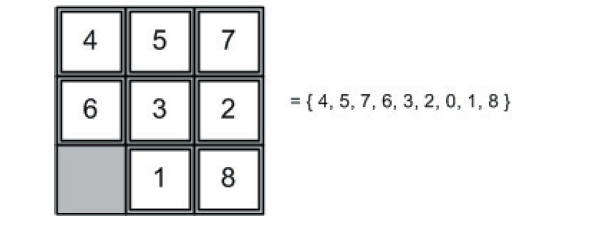
Ми будемо використовувати загальне уявлення для Загадки Восьми, лінійний вектор, що містить розташування черепиці зліва направо, зверху вниз (див. Малюнок 3.5). Ця конкретна фігура показує можливі рухи від початкової конфігурації головоломки до другої глибини цього конкретного дерева символів структури.
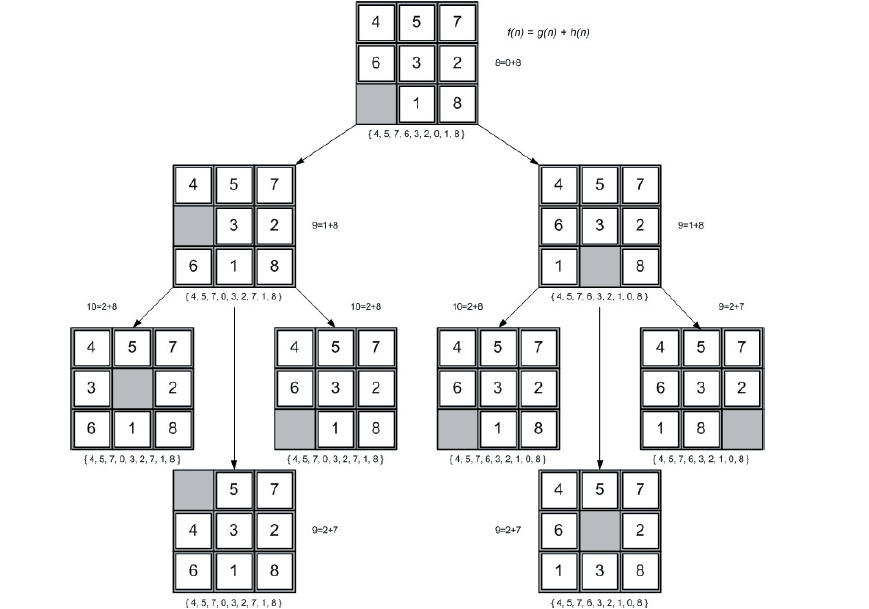
Для нашого евристичного методу ми будемо використовувати глибину дерева як вартість від кореневого до поточного вузла (інакше як g (n)), а також кількість неправильних плиток (h (n)) як оцінювану вартість для цільового вузла (крім порожнього). Вартість шляху (f (n)) потім стає вартістю шляху до поточного вузла (g (n)) плюс приблизна вартість цільового вузла (h (n)). Ви можете побачити ці евристики в дереві на малюнку 3.6. З кореневого вузла можливі лише два рухи, але з цих двох рухів відкриваються три нових ходи (стани). У нижній частині цього дерева ви можете побачити, що функція витрат зменшилася, що вказує на те, що ці конфігурації плану, швидше за все, будуть кандидатами для вивчення далі.
ПРИМІТКА Існує дві популярні евристики для проблеми N-головоломки. Перше - це просто кількість плиток, які не використовуються, що загалом зменшується, коли наближається ціль. Інший евристичний - це відстань Манхеттена від плитки, яка підсумовує відстань між черепицею кожної місцевої плитки та її правильному розташуванню. Для цієї реалізації ми продемонструємо просту, але ефективну елітарну схему.
Малюнок 3.6: Дерево Загадки Восьми завершуеться на другій глибині, ілюстрування функцій вартості.
Порада Хоча є (3 * 3)! можливі конфігурації плати, є лише (3 * 3)! / 2 дійсних конфігурацій. Інша половина конфігурацій нерозв'язна. Ми не зупинимося на цьому тут, але в реалізації джерела ви побачите тест у initPuzzle, використовуючи поняття інверсій для перевірки конфігурації плати. Цю концепцію можна детальніше дослідити в [KGong 2005].
Демонстрація Загадки Восьми з пошуком A *.
У процесі виконання плитки позначаються як A-H з пробілом, який використовується для позначення порожньої плитки. Після виконання, коли знайдено рішення, перераховується шлях, знятий з початкової плати до мети. Це показано нижче в нонатці, мінімізоване для простору.
Нотатка: Зразок програми А* для вирішення Загадки Восьми.
$./astar GBD FCH EA BGD FCH E A BGD FCH EA GBD FC EAH ... ABC DF GEH ABC D F GEH ABC DEF G H ABC DEF GH
Виконала Назаренко Валерія