Пошук Табу!!!

Це дуже простий алгоритм пошуку, який легко реалізувати і може бути дуже ефективним. Основна ідея пошуку Tабу - це пошук сусідів за допомогою списку Табу з вузлів, який складається з раніше оцінених вузлів. Тому пошук може погіршуватися, але це дозволяє алгоритму розширювати пошук, щоб уникнути затримки в локальних максимумах. Під час кожної ітерації алгоритму поточний кандидат пошуку порівнюється з найкращим рішенням, отриманим до цих пір, щоб кращий вузол зберігався пізніше. Після того як деякі критерії пошуку були виконані (знайдене рішення або максимальна кількість ітерацій), алгоритм виходить. Список Табу може бути встановленого розміру, щоб можна було видалити найстаріші вузли, що дає змогу створювати нові вузли Tабу. Вузли у списку Табу також можуть бути синхронізовані, тому що вузол може бути тільки Taбу протягом певного періоду часу.У будь-якому випадку алгоритм дозволяє повторно використовувати список Taбу і мінімізувати обсяг необхідної пам'яті.
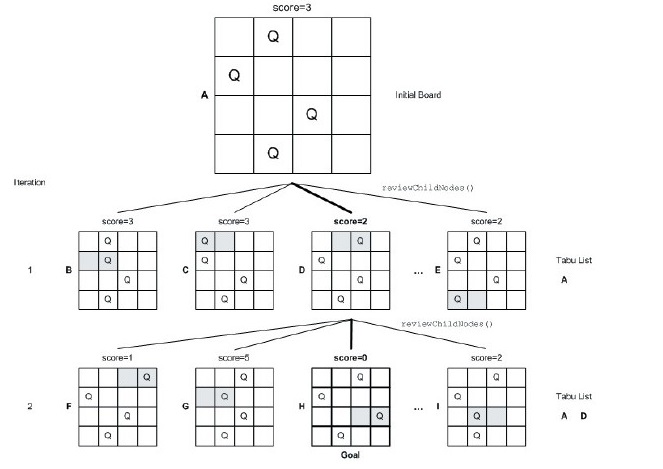
Моніторинг Taбу пошуку через пробіл у стані задачі 4-королев показаний на малюнку. Початкове положення - це корінь, яка має оцінку три (три конфлікти). Мета полягає в тому, щоб звести до мінімуму рахунок, де нуль - це рішення (цільовий вузол). На першій ітерації сусідні вузли оцінюються, а найкраще вибираються. Зауважте також, що наш початковий вузол був поміщений у список Taбу. При ітерації два, сусіди оцінюються за поточним вузлом, а найкраще - для переміщення вперед. Список Taбу тепер містить попередні два найкращі вузли. У цій ітерації ми знайшли вузол з оцінкою нуля, що вказує на цільовий вузол, і алгоритм закінчується. Основний потік пошуку Taбу показано у нотатці 3.14. Враховуючи початкову позицію (показану тут як початкову випадкову позицію), простір пошуку перераховується, беручи найкращий сусідній вузол, який не є Табу. Якщо це краще, ніж наше найкраще збережене рішення, це стане найкращим рішенням. Процес продовжується з останнім рішенням, доки не будуть виконані критерії завершення.
Нотатка: Базовий потік алгоритму пошуку Табу.
tabu_search()
{
cur_solution = random()
evaluate_position( cur_solution )
best = cur_solution
tabu( cur_solution )
while (!termination_critera) {
/* Get the best neighbor, not on the tabu list */
cur_solution = best_non_tabu_neighbor( cur_solution )
evaluate_position( cur_solution )
tabu( cur_solution )
if (cur_solution.f < best.f) {
best = cur_solution
}
}
return best
}
Щоб ілюструвати алгоритм пошуку Taбу, ми будемо використовувати задачу N-королев, як показано на першому алгоритмі пошуку. (Див. Малюнок 3.1 для резюме задачі та бажаного рішення.) Після обговорення основної реалізації табу, ми розглянемо деякі варіанти, які покращують алгоритм.
Втілення пошуку табу
Алгоритм пошуку Taбу дуже простий і може бути проілюстрований в одній функції (див. Нотатка, функція tabu_s). Ця функція є ядром алгоритму пошуку Taбу.
Реалізація починається з висіву випадкової функції (RANDINIT), після чого створюється черга Taбу. Ця черга являє собою список Taбу або ті елементи, які не будуть оцінюватися далі якщо його знову відкрили. Потім початкове рішення створюється та копіюється в найкраще рішення (через initBoard, щоб створити рішення, і оцінити таблицю, щоб оцінити значення рішення). Поточне рішення потім завантажується до списку Taбу так, що його знову не оцінюють.
Потім починається цикл, для якого ми будемо працювати вічно, або поки не знайдеться рішення. Для цієї простої проблеми ми завжди знайдемо рішення у певній кількості ітерацій. Заклик до reviewChildNodes оцінює сусідні рішення та вибирає найкращий, який не знаходиться в списку Taбу. Це рішення повертається (за посиланням), а потім завантажується в список Taбу. Зауважте, що ми спершу перевіримо, чи це вже в списку Taбу. Якщо ні, ми перевіряємо стан списку Taбу. Якщо повно, нам потрібен найстаріший елемент, щоб полегшити новий вузол, а потім додати його до черги.
Примітка Нагадаємо, що черги мають характер FIFO.Тому видалення вузла з черги автоматично видаляє найстаріший вузол, що задовольняє політику для алгоритму (видаліть найстаріший вузол першим, якщо список Taбу заповнений).
Нарешті, ми перевіряємо значення рішення, а якщо нуль, то ми маємо цільовий вузол. Тепер це може бути випущено за допомогою функції emitBoard.
Нотатка: Алгоритм базового пошуку Табу, реалізація на С.
void tabu_s()
{
unsigned short best_sol, cur_sol;
int best_f, cur_f;
RANDINIT();
tabu_q = createQueue(MAX_ELEMENTS);
/* Get initial board */
cur_sol = best_sol = initBoard();
cur_f = best_f = evaluateBoard( best_sol );
enQueue( tabu_q, best_sol );
while( 1 ) {
printf(“Iteration for %x\n”, cur_sol);
/* Return (by reference) the best non-tabu neighbor */
reviewChildNodes( &cur_sol, &cur_f );
/* Add the current best solution to the tabu list (remove
* the oldest if needed).
*/
if (!searchQueue( tabu_q, cur_sol )) {
if (isFullQueue( tabu_q )) {
(void)deQueue( tabu_q );
}
enQueue( tabu_q, cur_sol );
}
/* Save the best solution so far */
if (cur_f <= best_f) {
best_sol = cur_sol;
best_f = cur_f;
}
/* Solution found? */
if (best_f == 0 ) {
emitBoard( best_sol );
break;
}
}
destroyQueue( tabu_q );
return;
}
Демонстрація пошуку Taбу
Приклад пошуку Taбу ефективно знаходить рішення цієї проблеми (простір стану 256 унікальних вузлів). Перший evaluBoard - це початковий вузол (див. Нотаткy), а потім чотири ітерації алгоритму. Зауважте, що в той час, коли початковий вузол мав вартість двох, наступні оцінені вузли були гіршими, але в кінцевому підсумку призвели до мети. Пошук Табу дозволяє оцінювати від місцевого мінімуму, щоб визначити глобальний мінімум, як показано тут.
Нотатка: Приклад виконання пошуку Табу для вирішення задачі 4-королев.
evaluateBoard 1281 = (f 2) Iteration for 1281 evaluateBoard 2281 = (f 2) evaluateBoard 2181 = (f 3) evaluateBoard 2481 = (f 3) evaluateBoard 2241 = (f 2) evaluateBoard 2221 = (f 3) evaluateBoard 2281 = (f 2) evaluateBoard 2282 = (f 3) Iteration for 2281 evaluateBoard 4281 = (f 1) evaluateBoard 4181 = (f 1) evaluateBoard 4481 = (f 3) evaluateBoard 4281 = (f 1) evaluateBoard 4241 = (f 3) evaluateBoard 4282 = (f 2) Iteration for 4281 evaluateBoard 8281 = (f 2) evaluateBoard 8181 = (f 3) evaluateBoard 8481 = (f 4) evaluateBoard 8241 = (f 2) evaluateBoard 8221 = (f 3) evaluateBoard 8281 = (f 2) evaluateBoard 8282 = (f 2) Iteration for 8282 evaluateBoard 4282 = (f 2) evaluateBoard 2282 = (f 3) evaluateBoard 4182 = (f 0) evaluateBoard 4482 = (f 2) evaluateBoard 4282 = (f 2) evaluateBoard 4142 = (f 2) evaluateBoard 4181 = (f 1) evaluateBoard 4184 = (f 3) solution is 0x4182 0 1 0 0 0 0 0 1 1 0 0 0 0 0 1 0
Варіанти пошуку Taбу
Щоб зробити пошук Tabu більш ефективним для дуже складних пошукових завдань, існує ряд модифікацій. Перша з них називається інтенсифікацією і суттєво інтенсифікує пошук по певній точці (наприклад, найбільш відоме рішення). Ідея полягає в тому, що ми беремо перспективний вузол і поглиблюємо пошук по цій точці. Це реалізується за допомогою проміжної пам'яті, яка містить сусідні вузли, щоб йти далі.
Одне з питань, яке виникає в алгоритмах локального пошуку, полягає в тому, що вони можуть застрягти в локальних оптимумах. Пошук Табу вводить поняття диверсифікації, що дозволяє алгоритму шукати вузли, які раніше не були вивчені, щоб розширити простір пошуку. Коли ми дотримуємося найкращих рішень, дуже можливо застрягти в місцевих оптимумах для складних проблем. Інший цікавий варіант називається релаксацією обмежень, що послаблює алгоритм вибору сусідства, щоб прийняти вузли нижчої якості в пошуковому просторі. Це дозволяє алгоритму розширювати пошук, щоб спуститися до менш якісних рішень у пошуках більш якісних рішень. [Gendreau 2002]
Виконала Назаренко Валерія