Пошук в графі з обмеженням глибини!!!

Порядок виконання пошуку з обмеженням глибини 2

Поняття

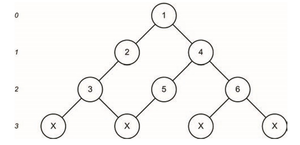
Пошук з обмеженням глибини (Depth-Limited Search, DLS) – це модифікація пошуку вглибину, яка мінімізує глибину, на яку може йти алгоритм пошуку. Крім того, що починається з кореневого та цільового вузлів, передбачається, що алгоритм не спускається нижче певного рівня. Ця модифікація зберігає алгоритм від безкінечних циклів, зупиняючи пошук після попередньо встановленої глибини.

Хоча алгоритм усуває можливість нескінченного циклу у графі, він також зменшує область пошуку. Якщо цільовий вузол був одним з вузлів із позначкою "X", його не було б знайдено, зробивши алгоритм пошуку неповним. алгоритм може бути повним, якщо глибина пошуку залежить від самого дерева (у цьому випадку d дорівнює трьом). Техніка також не є оптимальною, оскільки може бути знайдений перший шлях замість найкоротшого.

Час і простір обмеженого по глибині пошуку аналогічні DFS, з якого виводиться цей алгоритм. Складність простору - це O (bd), а складність часу - O (b^d), але в цьому випадку d є глибиною пошуку, а не графа.

Реалізація

#include <stdio.h> 
#include “graph.h” 
#include “stack.h” 
#define A 0 
#define B 1 
#define C 2 
#define D 3 
#define E 4 
#define F 5 
#define G 6 
#define H 7 
int init_graph( graph_t *g_p ) 
{
  addEdge( g_p, A, B, 1 );
  addEdge( g_p, A, C, 1 );
  addEdge( g_p, B, D, 1 );
  addEdge( g_p, C, E, 1 );
  addEdge( g_p, C, F, 1 );
  addEdge( g_p, D, G, 1 );
  addEdge( g_p, D, H, 1 );
  return 0; 
} 
void dls( graph_t *g_p, int root, int goal, int limit ) 
{
  int node, depth, to;
  stack_t *s_p, *sd_p;
  s_p = createStack( 10 );
  sd_p = createStack( 10 );
  pushStack( s_p, root );
  pushStack( sd_p, 0 );
  while ( !isEmptyStack(s_p) ) 
  {
    node = popStack( s_p );
    depth = popStack( sd_p );
    printf(“%d (depth %d)\n”, node, depth);
    if (node == goal) break;
    if (depth < limit) 
    {
      for (to = g_p->nodes-1 ; to > 0 ; to--) 
      {
        if (getEdge( g_p, node, to ) ) 
        {
          pushStack( s_p, to );
          pushStack( sd_p, depth+1 );
        }
      }
    }
  }
  destroyStack( s_p );
  destroyStack( sd_p );
  return; 
} 
int main() 
{
  graph_t *g_p;  g_p = createGraph( 8 );
  init_graph( g_p );
  dls( g_p, 0, 5, 2 );
  destroyGraph( g_p );
  return 0;
 }

Допоміжний АРІ

Для демонстрації алгоритмів пошуку необхідний допоміжний АРІ, що включає перелічені функції:

/* Graph API */ 
graph_t *createGraph (int nodes ); 
void destroyGraph (graph_t *g_p ); 
void addEdge (graph_t *g_p, int from, int to, int value ); 
int getEdge (graph_t *g_p, int from, int to ); 
/* Stack API */ 
stack_t  *createStack (int depth ); 
void destroyStack (stack_t *s_p ); 
void pushStack (stack_t *s_p, int value ); 
int popStack (stack_t *s_p ); 
int isEmptyStack (stack_t *s_p ); 
/* Queue API */ 
queue_t  *createQueue (int depth ); 
void destroyQueue (queue_t *q_p ); 
void enQueue (queue_t *q_p, int value ); 
int deQueue (queue_t *q_p ); 
int isEmptyQueue (queue_t *q_p ); 
/* Priority Queue API */ 
pqueue_t *createPQueue (int depth );
void destroyPQueue (pqueue_t *q_p ); 
void enPQueue (pqueue_t *q_p, int value, int cost ); 
void dePQueue (pqueue_t *q_p, int *value, int *cost ); 
int isEmptyPQueue (pqueue_t *q_p ); 
int isFullPQueue (pqueue_t *q_p );

Виконав Романів Роман

Developed by Інститут Програмних Систем