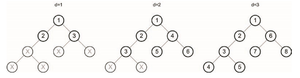
Пошук в графі з ітеративним заглибленням!!!

Порядок виконання пошуку з ітеративним заглибленням

Поняття

Пошук з ітеративним заглибленням (Iterative Deepening Search, IDS) – це похідний від DLS алгоритм, що поєднує в собі особливості пошуку вглибину з та пошуку вширину. IDS працює, виконуючи пошуки DLS із збільшеною глибиною, доки не буде знайдено ціль. Мінімізуючи глибину пошуку, ми змушуємо алгоритм шукати вширину графа. Якщо ціль не знайдено, збільшується глибина, яку алгоритму дозволено шукати, і він запускається знову.

IDS є зручним, тому що він не схильний до зациклення (характеристика DLS, на якій вона заснована). Він також знаходить ціль, найближчу до кореневого вузла, як і алгоритм BFS (який буде детально описано далі). З цієї причини це найкращий алгоритм, коли глибина рішення невідома.

Складність часу для IDS ідентична DFS і DLS, O (b^d). Простір складності IDS - O (bd). Навідмінно від DFS та DLS, IDS завжди знайде найкраще рішення, тому він є повним і оптимальним.

Реалізація

#include <stdio.h> 
#include “graph.h” 
#include “stack.h” 
#define A 0 
#define B 1 
#define C 2 
#define D 3 
#define E 4 
#define F 5 
#define G 6 
#define H 7 
int init_graph( graph_t *g_p ) 
{
  addEdge( g_p, A, B, 1 );
  addEdge( g_p, A, C, 1 ); 
  addEdge( g_p, B, D, 1 );
  addEdge( g_p, C, E, 1 );
  addEdge( g_p, C, F, 1 );
  addEdge( g_p, D, G, 1 );
  addEdge( g_p, D, H, 1 );
  return 0;
} 
int dls( graph_t *g_p, int root, int goal, int limit ) 
{
  int node, depth;
  int to;
  stack_t *s_p, *sd_p;
  s_p = createStack( 10 );
  sd_p = createStack( 10 );
  pushStack( s_p, root );
  pushStack( sd_p, 0 );
  while ( !isEmptyStack(s_p) )
  {
    node = popStack( s_p );
    depth = popStack( sd_p );
    printf(“%d (depth %d)\n”, node, depth);
    if (node == goal) return 1;
    if (depth < limit) 
    {
      for (to = g_p->nodes-1 ; to > 0 ; to--) 
      {
        if (getEdge( g_p, node, to ) ) 
        {
          pushStack( s_p, to );
          pushStack( sd_p, depth+1 );
        }
      }
    }
  }
  destroyStack( s_p );
  destroyStack( sd_p );
  return 0;
 }
 int main() 
{
  graph_t *g_p;
  int     status, depth;
  g_p = createGraph( 8 );
  init_graph( g_p );
  depth = 1;
  while (1) 
  {
    status = dls( g_p, 0, 5, depth );
    if (status == 1) break;
    else depth++;
  }
  destroyGraph( g_p );
  return 0;
}

Допоміжний АРІ

Для демонстрації алгоритмів пошуку необхідний допоміжний АРІ, що включає перелічені функції:

/* Graph API */ 
graph_t *createGraph (int nodes ); 
void destroyGraph (graph_t *g_p ); 
void addEdge (graph_t *g_p, int from, int to, int value ); 
int getEdge (graph_t *g_p, int from, int to ); 
/* Stack API */ 
stack_t  *createStack (int depth ); 
void destroyStack (stack_t *s_p ); 
void pushStack (stack_t *s_p, int value ); 
int popStack (stack_t *s_p ); 
int isEmptyStack (stack_t *s_p ); 
/* Queue API */ 
queue_t  *createQueue (int depth ); 
void destroyQueue (queue_t *q_p ); 
void enQueue (queue_t *q_p, int value ); 
int deQueue (queue_t *q_p ); 
int isEmptyQueue (queue_t *q_p ); 
/* Priority Queue API */ 
pqueue_t *createPQueue (int depth );
void destroyPQueue (pqueue_t *q_p ); 
void enPQueue (pqueue_t *q_p, int value, int cost ); 
void dePQueue (pqueue_t *q_p, int *value, int *cost ); 
int isEmptyPQueue (pqueue_t *q_p ); 
int isFullPQueue (pqueue_t *q_p );

Виконав Романів Роман

Developed by Інститут Програмних Систем