Robot Path Planning!!!

Зміст
Введення
Robot Path Planning (RPP) у динамічних середовищах - це проблема пошуку, заснована на вивченні шляхів без зіткнень за наявності динамічних та статичних перешкод. Багато методів були розроблені, щоб вирішити цю проблему. Пастки в локальних мінімумах і підтримка продуктивності в режимі реального часу відомі, як дві найбільш важливі проблеми, з якими стикаються ці методи. RPP планує поведінку робота, щоб він міг виконувати завдання. Отже, якщо поточний стан робота вважається початковим станом і станом робота після завершення завдання як кінцевий стан, RPP повинен планувати пошук можливого шляху і через цей шлях; робот зможе досягти кінцевого стану. RPP вивчається в різних середовищах, таких як статичне середовище,статичне середовище містить рухливі перешкоди, динамічне середовище містить статичні та динамічні перешкоди. У цих середовищах шлях динамічних перешкод невідомий і відомий як найважча проблема пошуку в порівнянні з іншими середовищами. У динамічних середовищах автономні роботи повинні надійно переміщатися між динамічними і статичними перешкодами. У динамічних середовищах було запропоновано дві проблеми, що стоять перед RPP. Це пастки в локальних мінімумах та підтримання ефективності в реальному часі.
Прикладні алгоритми для вирішення проблем планування шляху
Декілька підходів використовуються для вирішення проблеми планування маршруту в динамічному середовищі,які зображені на малюнку 3.1. Дивлячись на це зображення, методи та алгоритми поділяються на 3 категорії: Евристичні методи(Heuristic methods), Випадково вибіркові методи(Randomized Sampling methods) та Реактивний методи(Reactive methods).
Heuristic methods
Евристичні методи розглядаються багатьма дослідниками і значною мірою проводяться багатьма дослідженнями. Проста ідея для знаходження шляху є застосування базового алгоритму пошуку з рівномірною вартістю. Хоча цей метод пошуку є повним і оптимальним, він розширює багато вузлів, які недуже близькі до шляху розв'язку. Евристична функція - це альтернативний метод, який дозволяє оцінити найменш витратний маршрут від будь-якого вузла в пошуковому просторі до цілі. Евристична функція розроблена на основі проблем обмежень. Крім того, евристична функція спрямовує пошук до мети, не розширюючи багатьох вузлів, відвіданих найменш витратним пошуком. Тому евристична функція здатна скоротити час пошуку та використовуватися як алгоритм пошук в реальному часі. Ця категорія поділяється на три класи; а саме - евристичні(Heuristic), неавтономні(On-Line) та автономні(Off-Line). Неавтономні методи поділяються на евристичний пошук в реальному часі(Real-Time Heuristic) та класи алгоритмів будь-якого часу(Any-Time).
Heuristic
Проста прямолінійнна дистанційна евристична функція та статична 2D Dijkstra є двома евристичними функціями, які використовуються для RPP. Хоч ці методи оцінюють відстань від будь-якого стану до цілі, що є допустимою вони страждають від локальних мінімумів, що з'явилися через статичні перешкоди. Алгоритм A* є найвідомішим алгоритмом евристичного пошуку. У цьому алгоритмі є два списки, що називаються відкритими та закритими списками. Відкриті списки зберігають і замовляють всі стани, які знайдені та згенеровані А*. Відкритий список реалізується за списком пріоритетних черг. Евристична функція, яка використовується для A* є f(n), то ця функція для вузла n виглядає наступним чином:
f(n) = g(n) + h(n)
Там, де g(n) (cost-so-far) обчислюється вартість переходу від початкового вузла до вузла n, а h(n) (cost-to-go) оцінюється вартість для досягнення цілі з вузла n. Додавши кожен стан до відкритого списку, цей список повторно упорядковує свої записи за допомогою f-значень поступово. Таким чином, верхня частина списку відноситься до найменшого значення f. Слід зазначити, що записи з однаковими значеннями f відсортуються до більш високого gs. Після закінчення пошуку A* з'являється стан, який знаходиться у верхній частині відкритого списку, а потім зберігається в закритий список. Тому закритий список містить вибрані стани по А*. Цей алгоритм не здатний підтримувати роботу робота в режимі реального часу та легко потрапляє в пастку в локальних мінімумах. The Weighted A* є версією A*. Цей алгоритм використовує зважену евристичну функцію:
f(n) = g(n) + w.h(n)
Хоча більш високе значення w робить пошук більш жадібним, що зменшує час пошуку, цей метод має такі ж проблеми, як A* для динамічних середовищ.
Incremental Algorithm
Інкрементний евристичний алгоритм пошуку знаходить припустимий незаблокований шлях від його поточної клітинки до цільової комірки. Цей пошук виконується ітеративно, доки робот не досягне цілі або не стикнеться з заблокованою клітиною. Інкрементні алгоритми, які використовуються в галузі планування шляху, класифікуються на 3 групи. Перша група містить алгоритми, які є додатковими версіями A*. FSA* є одним з важливих алгоритмів цього класу. Механізм цього методу - це знайти найкоротший шлях від початку вузла до цілі з використанням A*. Алгоритм використовує попередній граф пошуку A*, який ідентичний поточному A* графу пошуку, для знаходження іншого короткого шляху між початковим та кінцевим станами, якщо деякі події позначені як статичні перешкоди. Друга група дізнається h-значення вузлів з попереднього пошуку та робить оцінку кращою. При оновленні h-значення, пошуковий алгоритм здатний вийти з локального мінімуму. Адаптивний A* є інкрементним алгоритмом, який розміщений у другій групі. Третя група змінює g-значення на основі попереднього пошуку. Ця група є більш ефективною групою в порівнянні з іншими групами, Differential A*, Focused Dynamic (D*) і D* Lite. У цій групі D* і D* Lite є більш складними, ніж Differential А*. В марсоходах та у проектах тактичних мобільних роботів, D* використовується для планування руху мобільних роботів. Ці алгоритми мають низьку продуктивність в умовах локальних мінімумів, і вони не можуть гарантувати продуктивність в режимі реального часу в динамічних середовищах.
On-Line
Алгоритми пошуку в реальному часі мають постійний зв'язок зі своїми середовищами, і вони здатні відстежувати зміни середовища, тому алгоритми пошуку в реальному часі є підходящими методами для вирішення проблем пошуку, коли робот спочатку має неповну інформацію про його оточення. У алгоритмах пошуку в режимі реального часу існує дві фази: 1) фаза планування, та 2) фаза дії. На етапі планування, робот обирає одну або декілька можливих дій (етап відбору) та оновлює евристичні значення вибраних станів (крок навчання), а потім виконує їх на етапі дії. Цей процес повторюється безперервно до тих пір, поки не досягне цілі. У фазі дії, робот здатний спостерігати за навколишнім середовищем та оновлювати інформацію про таке середовище.
Real-Time Heuristic
Першим алгоритмом реального часу є learning real-time A*(LRTA*). Було введено кілька модифікованих версій LRTA*. У фазі планування, LRTA* спочатку генерує спадкоємців поточної позиції робота і за допомогою алгоритму A* вибирає найкращих спадкоємців серед усіх спадкоємців. На етапі навчання він оновлює евристичні значення обраних спадкоємців. Цей метод може знайти найближчий оптимальний шлях швидше, ніж автономний метод. Механізм LRTA* дуже бідний, коли стикається з динамічними середовищами, і це має високу вартість рішення. Хоча структура LRTA*(k) подібна до LRTA*, цей алгоритм використовує інший підхід, ніж LRTA* для оновлення евристичних значень. Використовуючи більше знань, LRTA*(k) може вийти з локальних мінімумів. Цей алгоритм має дуже низьку продуктивність у поєднанні з динамічними середовищами. LRTALS(k,d) - модифікована версія LRTA*(k). Механізм навчання цього алгоритму покращується завдяки збільшенню рівня Lookahead та збільшенню рівня навчання на кожній фазі планування. На основі виконання цього методу він може планувати високошвидкісний рух, але цей алгоритм не може гарантувати продуктивність в режимі реального часу. Local Search Space Learning Real-Time A* (LSSLRTA*) відомий як найсучасніший алгоритм. У частині вибору, робот вибирає граничне число станів (LookAhead) і цей набір вузлів називається локальним пошуковим простором. Після вибору станів та збереження їх у закритому списку LSSLRTA* вибирає локальну ціль із станів, які зберігаються у відкритому списку. Стан з найменшим f-значенням є алгоритмічним кандидатом для локальної цілі. У навчальному розділі, алгоритм використовує алгоритм Dijkstra для зміни евристичних значень закритого списку. Використовуючи цей механізм навчання, LSSLRTA* може вийти з локальних мінімумів. Недоліком цього алгоритму є те, що він не може гарантувати продуктивність в режимі реального часу. RTD* - найсучасніший алгоритм для динамічних середовищ. Цей метод поєднує в собі D* Lite та LSS-LRTA*. Етап планування в цьому методі ділиться на дві частини: 1) D* Lite. 2) LSS-LRTA*. У першій частині RTD* повертається із стану цілі до поточного стану робота, і якщо він може знайти повний шлях, то повертає оптимальний шлях; Інакше LSS-LRTA* запуститься, щоб знайти відповідну дію в час, що залишився від часу планування. Недолік цього алгоритму повертається до D* Lite, оскільки цей алгоритм не може планувати високошвидкісні дії та він легко допустить помилку в багато-розмірному просторі станів. PLRTA* - це нова версія LSS-LRTA*. Цей метод, розділяючи витрати на статичні та динамічні, намагається вивчити їх окремо. Цей алгоритм має більш високу продуктивність у порівнянні з іншими алгоритмами евристичного пошуку в режимі реального часу в умовах динамічного середовища. Крім того, цей алгоритм гарантує продуктивність в режимі реального часу. Як зазначалося раніше, пастки в локальних мінімумах є одним з важливих завдань у цій галузі. Ця проблема трапляється, коли роботи потрапляють в пастку в регіонах евристичної депресії. Регіонами евристичної депресії називаються обмежені області пошукового простору, в яких евристична функція є неточною, а евристичні функції в реальному часі легко потрапляють в пастку в цих регіонах, оскільки евристичні значення їх станів можуть потребувати оновлення декілька разів, що призводить до дорогих рішень. Евристична депресивна область - це обмежена область, для якої евристичне значення станів на межі області більше або дорівнює евристичному значенню станів всередині регіону. Це визначення представляє два нові методи алгоритмів пошуку в реальному часі. Ці методи - Mark-and Avoid і Move-to-Border, вони застосували ці методи на LSSLRTA* і RTAA* представили 4 нових модифікованих версії, найкраща з яких називається daLSS-LRTS*. Механізм цих нових алгоритмів щодо вирішення регіонів евристичної депресії позначає стани всередині евристичної депресії, а потім уникає їх у наступних ітераціях. Виходячи з результатів, Move-to-Border є кращою технікою, і причина полягає в тому, що ця методика керує пошуком переміщуючи його до межі або до станів, які знаходяться ближче до межі. Хоча ці нові версії уникають локальних мінімумів, що покращує продуктивність алгоритму у порівнянні з іншими алгоритмами пошуку в режимі реального часу, нові версії, як оригінальна версія не можуть гарантувати продуктивність в режимі реального часу.
Any-Time
Алгоритми будь-якого часу намагаються покращити свої рішення з плином часу. Такі алгоритми можуть навіть повертати часткове рішення до будь-якого переривання в будь-який час. Якість відповідей, згенерованих цими алгоритмами, безпосередньо залежить від часу обчислення. Це означає, що згенерований розв'язок за допомогою алгоритму будь-якого часу є наближення оптимального або найкращого рішення та підвищення якості рішення шляхом додавання часу обчислень.Цей метод корисний для вирішення задач, що залежать від часу.Вони досягають великого успіху, використовуючи Anytime Repairing A* (ARA*).
Off-Line
Автономні алгоритми генерують всі шляхи від початкової позиції до позиції цілі на кожному кроці часу. Іншими словами, на відміну від інших методів, які генерують дію на кожному етапі часу, цей алгоритм має можливість генерувати повний шлях від початку до мети на кожному етапі. Етап планування в цьому методі повинен передбачати розташування рухомих об'єктів у шумному середовищі. Також обчислення планування є дорогим через час, який додається як змінна стану-простору. Тому для прогнозування траєкторії рухомого об'єкта необхідне перепланування. У цьому методі планування часу поділяється на два етапи часу. У першому етапі кожен стан представлений 5 кортежами (x, y, θ, v, t). На цьому етапі алгоритм прогнозує рух динамічної перешкоди до Tbmax, де прогноз є надійним. Якщо вони хочуть досягти прийнятної поведінки без зіткнення, вони повинні обмежити Tbmax. Це обмеження для планування часу дозволяє йому швидко перепланувати, що призводить до швидкої реакції на недавні зміни в навколишньому середовищі, після чого відбувається другий етап.У цьому методі алгоритм виконує планування до досягнення мети. Для пошуку оптимального шляху використовується пошук Weighted A*. Крім того, коли світовий простір стає більшим, а початкова позиція та позиція цілі розміщуватимуться далі один від одного, кількість часу зростатиме. Якщо кількість динамічних перешкод у навколишньому середовищі зростає, час планування збільшується. Важливим для цього методу є те, що, коли закінчується час, а потім пошук переходить на пошук 2D Dijkstra, цей метод буде захоплюватися в локальних мінімумах.Нова версія Accelerated A*(AA*), називається IAA*. Цей алгоритм, заснований на адаптивній вибірці, знімає баланс між швидкістю та точністю. IAA* з швидким методом планування є придатним для великих середовищ. Існує адаптивна параметризація, яка являє собою набір прийнятних дій руху транспортного засобу. У кожному поколінні ця адаптивна параметризація розглядається при розширенні дочірніх станів. Означає, що коли робот знаходиться далеко від перешкоди, алгоритм може зробити більший крок і зробити менший крок, коли робот знаходиться поруч із перешкодою. У цьому методі виконується кілька ітерацій пошуку, доки шлях не буде знайдений. Таким чином, незрозуміло, як алгоритм виділив час, пов'язаний з фазою планування, а також, якщо рішення не було знайдено до встановленого часу, алгоритм не знатиме, що має бути зроблено для наступного дії.
Randomized Sampling methods
Рандомізований підхід використовується для зменшення значної кількості досліджуваних станів під час пошуку. Цей підхід здатний легко обробляти ситуації, коли пошук стає неможливим через збільшенням простору станів та надто багатьох досліджених станів. Rapidly-Exploring Random Tree(RRT) - це рандомізований алгоритм вибірки. Механізм цього алгоритму для пошуку створює та розширюється за межі випадкового дерева з початкового стану. Хоча розширення дерева відбувається випадковим чином, нерозвідані регіони мають більше значення, ніж інші регіони, і алгоритм пошуку упереджений до них. RRT є одним з найвідоміших алгоритмів рандомізованих вибірок в роботизованому співтоваристві і цей алгоритм використовується в різних платформах робототехніки.RRT не може гарантувати виконання в реальному часі, і це продемонструвало найкраще рішення, яке вивчається даним алгоритмом, майже завжди є не оптимальним рішенням. Крім того, RRT не враховує витрати на розширення дерева; тому оснований шлях може бути розміщений у дорогих областях.Остання версія RRT - ERRT. Під час кожної ітерації пошуку ERRT записує деяку інформацію та використовує записану інформацію з попередньої ітерацій, щоб знайти кращий шлях. Алгоритм The Metric Adaptive RRT (MA-RRT) є модифікованою версією RRT. Цей алгоритм звертається до проблем RRT. MA-RRT, як і ERRT використовує інформацію про попередню ітерацію та за допомогою попередньої інформації, MA-RRT здатний керувати пошуком (дерева) у напрямках, де містяться кращі та найближчі оптимальні шляхи. RRT* має інший підхід до розширення дерева. За даними RRT*, дерево росте випадково через одну вершину. Також RRT* спочатку виростає дерево з однієї вершини і оцінює це розширення, і якщо розширення з цієї вершини вважається успішним, тоді RRT* прагне одночасно досліджувати і ростити дерево від усіх інших вершин де їх відстані до запропонованої вершини не перевищує певного порогу.Хоча цей алгоритм знаходить краще рішення, ніж RRT, особливо якщо час пошуку збільшується, він має високу обчислювальну вартість.
Reactive methods
Загалом, реактивні методи не виконують жодного пошуку, щоб знайти їх шлях. Замість пошуку вони використовують диференційовану функцію. Механізм цього методу ґрунтується на такому припущенні, що поверхня простору станів може бути картою для диференційованої функції, градієнт якої відхиляється від перешкод у напрямку до мети. Дії робота повинні сходитися до градієнту. Potential field – це один із алгоритмів цієї категорії. Основний недолік цієї категорії пастки в локальних мінімумах.
Поточні проблеми RPP
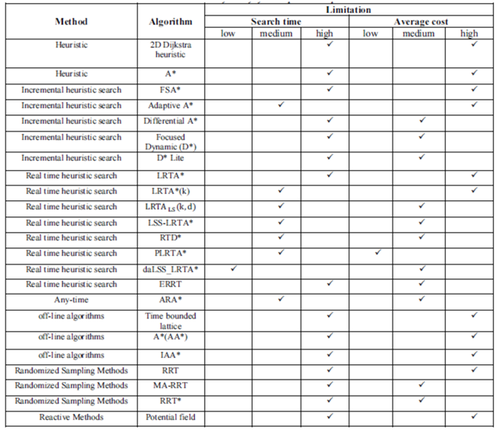
Таблиця,що знаходиться нижче, показує ефективність найбільш підходящих переглянутих підходів, що стоять перед двома проблемами. Ці дві проблеми - це пастки в локальних мінімумах та підтримка роботи в реальному часі. Як вже було сказано раніше, пастки в локальних мінімумах зумовлюють збільшення часу пошуку, і якщо механізм підходу не підтримує роботу в реальному часі, то середня вартість рішення зростає. Показано, що деякі алгоритми, такі як інкрементний евристичний пошук та алгоритми евристичного пошуку в режимі реального часу в цій галузі, є більш корисними і тому мають більш широкі можливості для проведення деяких досліджень про них. Крім того, ці алгоритми мають більш високу продуктивність в порівнянні з іншими алгоритмами, що стоять перед зазначеними проблемами. З іншого боку, здається, що кожен підхід, особливо реактивний метод, страждають від багатьох недоліків.
Виконав: Цимбаленко Денис