Пошук А*!!!

Зміст
Пошук А*. Загально
Пошук А*, як і«найкращий-перший» пошук, оцінює простір пошуку за допомогою евристичної функції. Але A * використовує як вартість отримання від початкового стану до поточного стану (g (n)), так і оцінювану вартість (евристичну) шляху від поточного вузла до мети (h (n)). Вони підсумовуються до функції витрат f (n). Пошук A *, на відміну від першого, є оптимальним і повним.
Списки OPEN та CLOSED знову використовуються для визначення межі пошуку (OPEN) та оцінених вузлів до цих пір (CLOSED). Список OPEN реалізується як пріоритетна черга, замовлена в нижчому порядку f (n). Що робить A * цікавим, що він постійно переоцінює функцію вартості для вузлів, коли вона повторює їх. Це дозволяє A * ефективно знайти мінімальний шлях від початкового стану до стану кінцевого. Давайте тепер подивимося на A * на високому рівні, а потім копатимемо далі і застосуємо його до загальновідомих проблем. Нотатка забезпечує високий рівень потоку для A *.
Нотатка: Висопопоточний алгоритм для пошуку А*.
Initialize OPEN list (priority queue) Initialize CLOSED list Place start node on the OPEN list Loop while the OPEN list is not empty Get best node (parent) from OPEN list (least f (n)) if parent is the goal node, done Place parent on the CLOSED list Expand parent to all adjacent nodes (adj_node) if adj_node is on the CLOSED list discard adj_node and continue else if adj_node is on the OPEN list if adj_node’s g value is better than the OPEN.adj_node’s g value discard OPEN.cur_node calculate adj_node’s g, h and f values set adj_node predecessor to parent add adj_node to OPEN list continue end else calculate adj_node’s g, h and f values set adj_node predecessor to parent add adj_node to OPEN list end end end loop
Зверніть увагу, як видно з нотатки, що як тільки ми виявимо найкращий вузол з списку OPEN, ми розкриємо всі дочірні вузли (можливі легальні структури з кращого вузла). Якщо нові легальні структури не знайдені в списках OPEN або CLOSED, вони додаються як нові вузли (встановлюючи попередник кращого вузла або предка). Якщо новий вузол знаходиться в списку CLOSED , то ми відкинемо його і продовжуватимемо. Нарешті, якщо новий вузол знаходиться у списку OPEN, але новий вузол має краще значення g, ми відкидаємо вузол у списку OPEN та додаємо новий вузол до списку OPEN (в іншому випадку новий вузол буде відкинутий, якщо його g значення гірше). Переоцінюючи вузли в списку OPEN та замінюючи їх, коли дозволяють функції витрат, ми дозволяємо вийти з простору структури кращими шляхами. Як ми вже визначили, A * є повним, поки пам'ять підтримує глибину та розгалуження дерева. А * також оптимально, але ця характеристика залежить від використання «прийнятної» евристики. Оскільки A * слід відстежувати поки що оцінені вузли (а також виявлені вузли, що підлягають оцінці), складність часу та простору є О (b^d).
ПРИМІТКА.
Евристичний визначається як допустимий, якщо він точно оцінює вартість шляху до цілі або її недооцінює (залишається оптимістичним). Це вимагає, щоб евристичний монотонний, що означає, що вартість ніколи не зменшується по шляху, а замість цього монотонно зростає. Це означає, що g (n) (шлях коштує від вихідного вузла до поточного вузла) монотонно зростає, а h (n) (шлях коштує від поточного вузла до цільового вузла) монотонно зменшується.
Пошук A * і Загадка Восьми
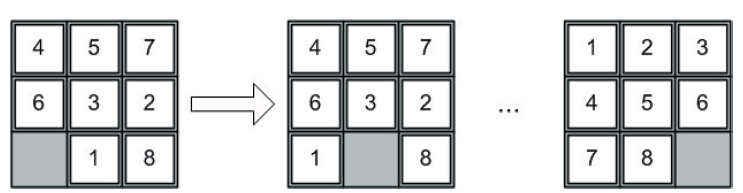
Хоча A * успішно застосовується до проблемних доменів, таких як конфігурація, ми застосуємо його тут, що називається "Загадка Восьми" (також відомий як N від M, або n^2-1 загадка черпиць). Ця особлива варіація головоломки складається з восьми черепиць в сітці 3х3. В одному місці немає плитки, що можна використовувати для переміщення інших плиток для переходу від однієї конфігурації до іншої (див. Малюнок 3.4).
Малюнок 3.4: Задача Восьми та демонстрація переходу з вхідної конфігурації до кінцевої (не включає кожен єтап).
Зверніть увагу на малюнку 3.4, що є можливі дві дії. Плитка '1' може рухатися вліво, а плитка '6' може рухатися вниз. Остаточна мета конфігурації показана справа. Зауважте, що це один варіант мети, і той, який ми будемо використовувати тут.
Загадка Восьми- це цікаво, тому що важко вирішити проблему, але та, що вивчається довго, і тому дуже добре зрозуміла. [Archer 1999] Наприклад, кількість можливих конфігурацій сітки Загадки Восьми (n * n)!, але лише половина з них є легальними конфігураціями. Підказка У 1870-х роках Загадка П'ятнадцяти (4 на 4 варіанти головоломки N по M) перетворилися на загальне захоплення так само, як кубик Рубіка 1970-х та 80-х років.
У середньому 22 кроки потрібні для вирішення 3-х варіантів головоломки. Але, розглядаючи 22 як середню глибину дерева, із середнім коефіцієнтом розгалуження 2,67, може бути оцінено 2,4 трильйони не унікальних плиток.
Пошук A *. Реалізація.
Основний алгоритм A* реалізовано в функції astar (). Ця функція реалізує A*, як показано в Нотатці 3.4. Ми також представимо функцію оцінки, яка реалізує показник "плитки за місцем". Список та інші функції підтримки не представлені тут, але доступні на компакт-диску для перегляду.
Почнемо з функції оцінки, яка обчислює орієнтовну вартість від поточного вузла до мети (у міру того як кількість плиток не використовується), див. Нотатка. Функція просто перераховує плату 3 на 3 в якості одномірного вектора, збільшуючи значення балів, коли плитка присутня в положенні, в якому воно не повинно бути. Це значення потім повертається абоненту.
Нотатка: Оціночна вартість показника h(n).
double evaluateBoard( board_t *board_p )
{
int i;
const int test[MAX_BOARD-1]={1, 2, 3, 4, 5, 6, 7, 8 };
int score=0;
for (i = 0 ; i < MAX_BOARD-1 ; i++) {
score += (board_p->array[i] != test[i]);
}
return (double)score;
}
Функція аstar показана в нотатці. Перед викликом цієї функції ми обрали випадкову конфігурацію дошки та розмістили її у списку OPEN. Потім ми працюємо через список OPEN, отримуючи найкращий вузол (з найменшим значенням f, використовуючи getListBest), і негайно поміщаємо його в список CLOSED. Ми перевіряємо, чи цей вузол є рішенням, і якщо це так, ми вилучаємо шлях від початкового вузла до мети (що ілюструє рухи, які були зроблені). Щоб мінімізувати пошук надто глибоко в дереві, ми зупиняємо перелік вузлів, що перевищують задану глибину (ми більше не шукаємо їх).
Наступним кроком буде перелік можливих кроків від цього стану, яких буде максимум чотири. Функція getChildBoard використовується для повернення сусіднього вузла (використовуючи індекс, що передається, для визначення можливого переміщення). Якщо переміщення неможливе, то повертається NULL, і його ігнорують.
За допомогою нового дочірнього вузла ми перевіряємо, чи вона вже була оцінена (якщо вона знаходиться в списку CLOSED). Якщо це так, ми повинні знищити цей вузол і продовжувати (щоб отримати дочірній вузол для поточної конфігурації дошки). Якщо ми раніше не бачили цю конкретну конфігурацію дошки, ми обчислюємо евристику для вузла. По-перше, ми ініціалізуємо глибину вузла в дереві як глибину предка плюс один. Далі, ми викликаємо evaluateBoard, щоб отримати метрику, що виходить за межі плитки, яка буде діяти як наша значення h (вартість від кореневого вузла до цього вузла). Значення g встановлюється на поточну глибину, а значення f ініціалізується за допомогою рівняння.
Тут ми включаємо параметри альфа та бета, щоб дати різну вагу для значень g та h. У цій реалізації альфа - 1,0, бета - 2,0. Це означає, що більша вага надається значенням h, а згодом, чим ближче до цілі вузол, він зважується вище його глибини в дереві стану. Коли обчислено значення f, ми перевіряємо, чи знаходиться вузол у списку OPEN. Якщо це так, ми порівнюємо їх значення f. Якщо вузол у списку OPEN має гірше значення f, вузол у списку OPEN відкидається, а новий дочірній вузол займає своє місце (встановивши посилання попередника на предка, тому ми знаємо, як ми перейшли до цього вузла). Якщо вузол у списку OPEN має краще значення f, то вузол у списку OPEN залишається у відкритому списку, а новий дочірній вузол відкидається. Нарешті, якщо новий дочірній вузол не існує ні в списку ЗАКРИТО, ні в OPEN, це новий вузол, який ми ще маємо побачити. Він просто додається до списку OPEN, і процес триває. Цей алгоритм продовжується до тих пір, поки не відбудеться одне з двох подій. Якщо список OPEN стає порожнім, то не знайдено жодного рішення, а алгоритм завершується. Якщо рішення знайдено, викликається showSolution, а вузли, з'єднані між собою через посилання попередника, перераховуються, щоб показати рішення від вихідного вузла до цільового вузла.
Нотатка: Алгоритм А*.
void astar( void )
{
board_t *cur_board_p, *child_p, *temp;
int i;
/* While items are on the open list */
while ( listCount(&openList_p) ) {
/* Get the current best board on the open list */
cur_board_p = getListBest( &openList_p );
putList( &closedList_p, cur_board_p );
/* Do we have a solution? */
if (cur_board_p->h == (double)0.0) {
showSolution( cur_board_p );
return;
} else {
/* Heuristic - average number of steps is 22 for a 3x3, so
* don’t go too deep.
*/
if (cur_board_p->depth > MAX_DEPTH) continue;
/* Enumerate adjacent states */
for (i = 0 ; i < 4 ; i++) {
child_p = getChildBoard( cur_board_p, i );
if (child_p != (board_t *)0) {
if ( onList(&closedList_p, child_p->array, NULL) ) {
nodeFree( child_p );
continue;
}
child_p->depth = cur_board_p->depth + 1;
child_p->h = evaluateBoard( child_p );
child_p->g = (double)child_p->depth;
child_p->f = (child_p->g * ALPHA) + (child_p->h * BETA);
/* New child board on the open list? */
if ( onList(&openList_p, child_p->array, NULL) ) {
temp = getList(&openList_p, child_p->array);
if (temp->g < child_p->g) {
nodeFree(child_p);
putList(&openList_p, temp);
continue;
}
nodeFree( temp );
} else {
/* Child board either doesn’t exist, or is better than a
* previous board. Hook it to the parent and place on the
* open list.
*/
child_p->pred = cur_board_p;
putList( &openList_p, child_p );
}
}
}
}
}
return;
}
A * варіанти
Популярність A * породила ряд варіантів, які пропонують різні характеристики. Алгоритм Ітеративне-поглиблення A * відступає до інших вузлів, коли вартість поточної гілки перевищує порогове значення. Щоб мінімізувати вимоги до пам'яті A *, було створено алгоритм спрощеного алгоритму A *, обмежений пам'яттю (SMA *). SMA * використовує доступну для нього пам'ять, і коли він виходить за межі доступної пам'яті, алгоритм знижує найменш перспективний вузол, щоб полегшити нові пошукові вузли з нової області.
Застосування пошуку A *
Пошук A * є популярною технікою та використовується як алгоритм визначення шляху для комп'ютерних стратегічних ігор. Для більшої продуктивності в багатьох іграх застосовуються більш прості способи швидкого пошуку шляху, обмежуючи простір їх переміщення (використовуючи набагато розріджений графік по ландшафту) або попередньо розраховуючи маршрути для використання в грі.
Виконала Назаренко Валерія